Exercise 3-21(2)
What equations are needed to add to the following graphs in order to present the associated preorders?
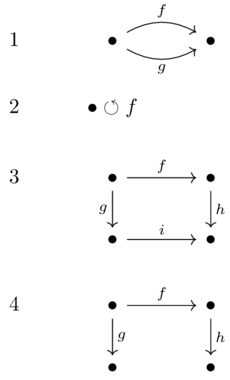
Solution(1)
f=g
f;f=f
f;h=g;i
none are needed
Takeaway: A preorder is a category where every two parallel arrows are the same.
Any preorder can be considered a category, and any category can be crushed down into a preorder (called preorder reflection).
The objects are the elements of the set, and there is a single morphism between a and b iff \(a \leq b\)
Considering a preorder as a category is right adjoint to turning a category into a preorder by preorder reflection.
Every category presentation lies somewhere between the free category and the preorder reflection.
What equations are needed to add to the following graphs in order to present the associated preorders?

f=g
f;f=f
f;h=g;i
none are needed
What is the preorder reflection of the category \(\mathbb{N}\) from Example 3.13
The trivial preorder of one object.